Appendix A:
Precession
 In Section 5.4, I briefly described the phenomenon of precession, which explains why the astrological “signs” of the Zodiac are now “out of step” with the corresponding constellations, and why the First Point of Aries, also known as the Vernal Equinox, is now in the constellation of Pisces. Here, for the benefit of those readers who might be interested, I’ll attempt to explain the physics of why precession happens.
In Section 5.4, I briefly described the phenomenon of precession, which explains why the astrological “signs” of the Zodiac are now “out of step” with the corresponding constellations, and why the First Point of Aries, also known as the Vernal Equinox, is now in the constellation of Pisces. Here, for the benefit of those readers who might be interested, I’ll attempt to explain the physics of why precession happens.
 As I said in Section 5.4, the Vernal Equinox moves steadily westwards along the Ecliptic at a rate of 50.27 arc seconds per year, completing a full circle every 25800 years. Since the astrologers’ “signs” – which are equal 30° sectors of the Ecliptic - are defined with respect to the Vernal Equinox, this means that they move with respect to the stars at the same rate; hence they move out of step with the constellations, at the rate of one “sign” every ( 25800 / 12 ) years.
As I said in Section 5.4, the Vernal Equinox moves steadily westwards along the Ecliptic at a rate of 50.27 arc seconds per year, completing a full circle every 25800 years. Since the astrologers’ “signs” – which are equal 30° sectors of the Ecliptic - are defined with respect to the Vernal Equinox, this means that they move with respect to the stars at the same rate; hence they move out of step with the constellations, at the rate of one “sign” every ( 25800 / 12 ) years.
 This phenomenon is called the Precession of the Equinoxes, usually just referred to as precession. It was discovered as long ago as 125 BC, by the Greek astronomer Hipparchus. While compiling his famous star catalogue, he found that the star positions recorded in a catalogue from a couple of centuries earlier were consistently in error. He correctly deduced that the relative positions of the Ecliptic and the Celestial Equator are constantly changing, with the Vernal Equinox moving westwards along the Ecliptic at the aforementioned rate. ( The Vernal Equinox, remember, is one of the two points at which the Ecliptic and Celestial Equator intersect. ) The Ecliptic, which is a great circle in the plane of the Earth’s orbit, is fixed with respect to the stars, and the Celestial Equator moves with respect to it.
This phenomenon is called the Precession of the Equinoxes, usually just referred to as precession. It was discovered as long ago as 125 BC, by the Greek astronomer Hipparchus. While compiling his famous star catalogue, he found that the star positions recorded in a catalogue from a couple of centuries earlier were consistently in error. He correctly deduced that the relative positions of the Ecliptic and the Celestial Equator are constantly changing, with the Vernal Equinox moving westwards along the Ecliptic at the aforementioned rate. ( The Vernal Equinox, remember, is one of the two points at which the Ecliptic and Celestial Equator intersect. ) The Ecliptic, which is a great circle in the plane of the Earth’s orbit, is fixed with respect to the stars, and the Celestial Equator moves with respect to it.
 Explaining why this happens had to wait another 1800 years, until Sir Isaac Newton came along! Precession, in general, is a phenomenon which can be easily demonstrated using a simple gyroscope, such as a child’s spinning top. Set the top spinning, then give it a slight nudge so that its axis of rotation tilts away from the vertical – but not far enough to make it topple over! The axis of rotation will then change direction periodically; its direction rotates around the vertical at a constant rate, so that the axis traces out a cone.
Explaining why this happens had to wait another 1800 years, until Sir Isaac Newton came along! Precession, in general, is a phenomenon which can be easily demonstrated using a simple gyroscope, such as a child’s spinning top. Set the top spinning, then give it a slight nudge so that its axis of rotation tilts away from the vertical – but not far enough to make it topple over! The axis of rotation will then change direction periodically; its direction rotates around the vertical at a constant rate, so that the axis traces out a cone.
 This is the reaction of any rotating object when an external torque ( turning effect of two forces ) is applied. In this case, the external torque is provided by gravity, and by the upward reaction of the floor on the base of the top. When the top is tilted, its weight, acting through its centre of mass, exerts a force vertically, at an angle to its axis of rotation ( Fig. 3 ). This force is now displaced horizontally from the upward reaction, and so these two forces – parallel and in opposite directions - create the torque.
This is the reaction of any rotating object when an external torque ( turning effect of two forces ) is applied. In this case, the external torque is provided by gravity, and by the upward reaction of the floor on the base of the top. When the top is tilted, its weight, acting through its centre of mass, exerts a force vertically, at an angle to its axis of rotation ( Fig. 3 ). This force is now displaced horizontally from the upward reaction, and so these two forces – parallel and in opposite directions - create the torque.
 This torque can’t speed up or slow down the top, but can change its direction of spin – just as the tension in the string of a whirling conker doesn’t change its speed, but does continually change its direction of motion, thus making it follow a circle. The directional effect of the torque is at right angles to itself, which means it’s perpendicular to the plane formed by the spin axis and the vertical. This causes the axis to precess, or rotate around the vertical.
This torque can’t speed up or slow down the top, but can change its direction of spin – just as the tension in the string of a whirling conker doesn’t change its speed, but does continually change its direction of motion, thus making it follow a circle. The directional effect of the torque is at right angles to itself, which means it’s perpendicular to the plane formed by the spin axis and the vertical. This causes the axis to precess, or rotate around the vertical.
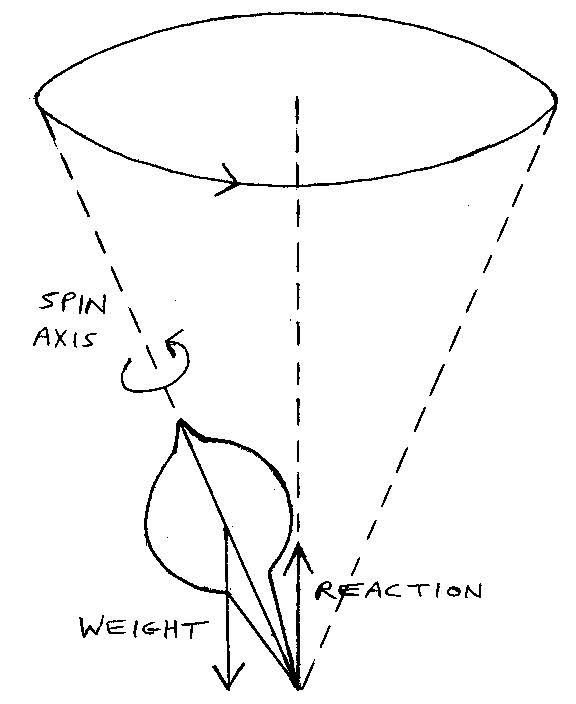
Fig. 3
 Now, as I hope you know, the Earth’s axis of rotation is tilted at an angle of 23.5° to the “vertical”, if we regard the plane of its orbit as the “horizontal” - so it behaves just like a tilted gyroscope ( Fig. 4 ). But what provides the external torque?
Now, as I hope you know, the Earth’s axis of rotation is tilted at an angle of 23.5° to the “vertical”, if we regard the plane of its orbit as the “horizontal” - so it behaves just like a tilted gyroscope ( Fig. 4 ). But what provides the external torque?
 Well, the Earth isn’t quite spherical; it’s actually an oblate spheroid, which means a slightly “squashed” sphere. Its diameter measured through the Equator is about 0.3% bigger then that measured through the poles. ( This is a consequence of its rotation. ) Combining this equatorial bulge ( shown in black in Fig. 4 ) with the tilt of its axis means that the gravitational attraction between the Earth and the Sun produces two “off-centre” forces, which create a torque, just like that acting on the spinning top. This torque acts as if it’s trying to “straighten” the tilt and pull the Equator into the plane of the Ecliptic, but its directional effect, as with the top, is at right angles to the plane containing the Earth’s axis and the Sun. So again, the effect of the torque is to cause the Earth’s axis to precess.
Well, the Earth isn’t quite spherical; it’s actually an oblate spheroid, which means a slightly “squashed” sphere. Its diameter measured through the Equator is about 0.3% bigger then that measured through the poles. ( This is a consequence of its rotation. ) Combining this equatorial bulge ( shown in black in Fig. 4 ) with the tilt of its axis means that the gravitational attraction between the Earth and the Sun produces two “off-centre” forces, which create a torque, just like that acting on the spinning top. This torque acts as if it’s trying to “straighten” the tilt and pull the Equator into the plane of the Ecliptic, but its directional effect, as with the top, is at right angles to the plane containing the Earth’s axis and the Sun. So again, the effect of the torque is to cause the Earth’s axis to precess.
 The Moon also contributes; the process is made very complicated by such factors as the Earth’s orbit being elliptical and the Moon’s orbit being inclined with respect to the Ecliptic. But the net result is that the axis precesses with a period of 25800 years. Consequently, the North Celestial Pole ( marked NCP in Fig. 4 ), traces out a circle on the sky – the Precessional Circle - over that same period, with a radius of 23.5°, and centred on the North Ecliptic Pole. The North Ecliptic Pole ( marked NEP in Fig. 4 ) is the pole of the Ecliptic great circle, i.e. the point “vertically” above the Ecliptic plane; this point is fixed with respect to the stars, and is located in the constellation of Draco.
The Moon also contributes; the process is made very complicated by such factors as the Earth’s orbit being elliptical and the Moon’s orbit being inclined with respect to the Ecliptic. But the net result is that the axis precesses with a period of 25800 years. Consequently, the North Celestial Pole ( marked NCP in Fig. 4 ), traces out a circle on the sky – the Precessional Circle - over that same period, with a radius of 23.5°, and centred on the North Ecliptic Pole. The North Ecliptic Pole ( marked NEP in Fig. 4 ) is the pole of the Ecliptic great circle, i.e. the point “vertically” above the Ecliptic plane; this point is fixed with respect to the stars, and is located in the constellation of Draco.
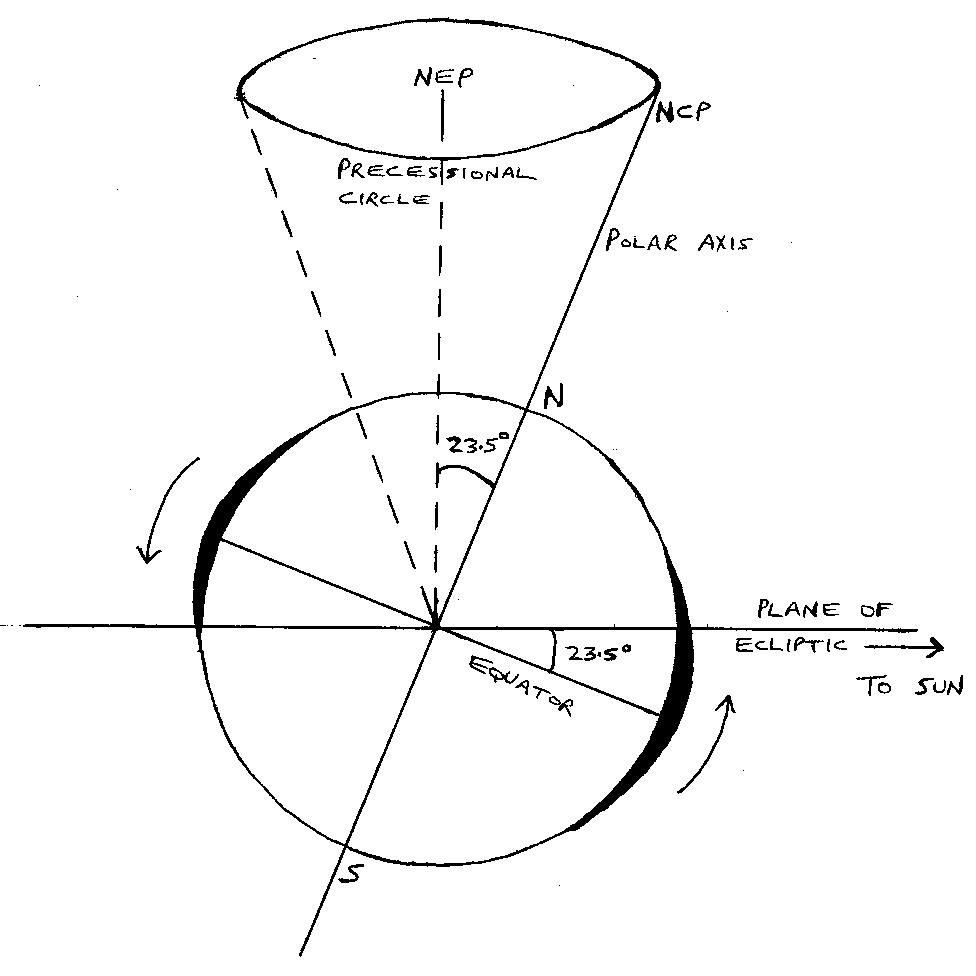
Fig. 4
 We are very fortunate, at the present time, to have a nice bright star, Polaris, which conveniently marks the North Celestial Pole for us; as we can now see, this situation is only temporary. Fig. 5 shows how the North Celestial Pole moves around the sky in the Precessional Circle. About 4500 years ago, when the Pyramids were built, Alpha Draconis, also known as Thuban, was the Pole Star, and was about as close to the true pole as Polaris is now. ( Indeed, we know that Thuban was very important in the culture of ancient Egypt; for example, a shaft in the Great Pyramid, which was meant to be the King’s route to Heaven, is precisely aligned with it. ) Around AD 7500, Alpha Cephei will make a pretty good Pole Star; by AD 14000, the nearest bright star to the pole will be Vega, though that will be much further from the true pole. And of course, Polaris will return to its current prominence 25800 years from now.
We are very fortunate, at the present time, to have a nice bright star, Polaris, which conveniently marks the North Celestial Pole for us; as we can now see, this situation is only temporary. Fig. 5 shows how the North Celestial Pole moves around the sky in the Precessional Circle. About 4500 years ago, when the Pyramids were built, Alpha Draconis, also known as Thuban, was the Pole Star, and was about as close to the true pole as Polaris is now. ( Indeed, we know that Thuban was very important in the culture of ancient Egypt; for example, a shaft in the Great Pyramid, which was meant to be the King’s route to Heaven, is precisely aligned with it. ) Around AD 7500, Alpha Cephei will make a pretty good Pole Star; by AD 14000, the nearest bright star to the pole will be Vega, though that will be much further from the true pole. And of course, Polaris will return to its current prominence 25800 years from now.

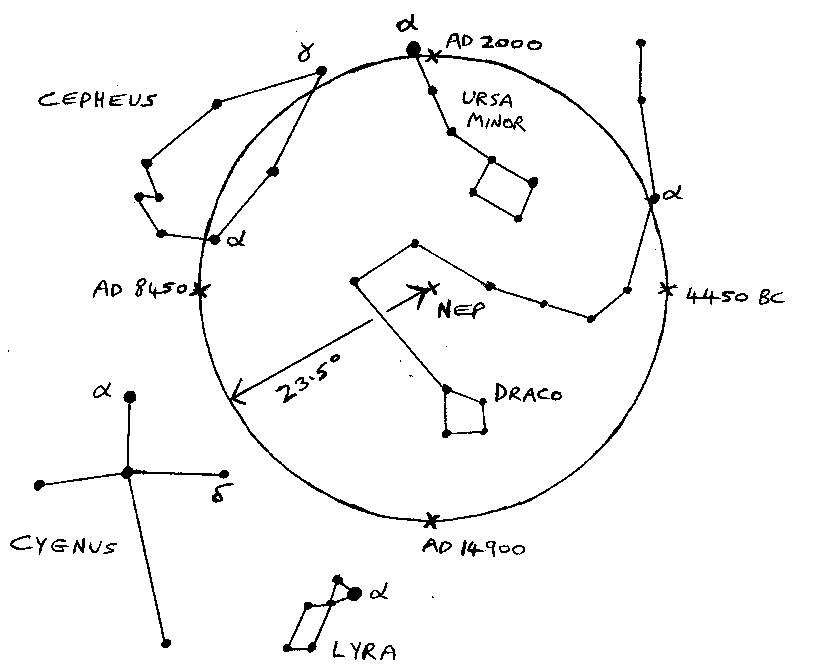
Fig. 5
 All of this has an important consequence for practical astronomy. As the direction of the Earth’s axis changes, so too does the plane of the Equator – hence the aforementioned movement of the Vernal Equinox along the Ecliptic. But right ascension and declination - the coordinates by which we describe an object’s position on the Celestial Sphere - are defined with respect to the Celestial Equator and the Vernal Equinox. Therefore, the right ascension and declination of every astronomical object also constantly change over that 25800 year period. This presents us with an obvious problem; our star atlases and catalogues soon become inaccurate! Indeed, it was this effect which first led Hipparchus to discover precession.
All of this has an important consequence for practical astronomy. As the direction of the Earth’s axis changes, so too does the plane of the Equator – hence the aforementioned movement of the Vernal Equinox along the Ecliptic. But right ascension and declination - the coordinates by which we describe an object’s position on the Celestial Sphere - are defined with respect to the Celestial Equator and the Vernal Equinox. Therefore, the right ascension and declination of every astronomical object also constantly change over that 25800 year period. This presents us with an obvious problem; our star atlases and catalogues soon become inaccurate! Indeed, it was this effect which first led Hipparchus to discover precession.
 For this reason, modern star atlases and catalogues always state the epoch for which they were produced, i.e. the particular point in time for which the coordinates given for objects were, or will be, absolutely correct. Most of them use “standard epochs”, which are usually multiples of 50 years; the positions of objects are plotted for the standard epoch closest to the date of publication. So atlases produced between 1925 and 1975 are plotted for “Epoch 1950.0”, i.e. they plot star positions as they were at the start of 1950. Those produced since 1975 are plotted for “Epoch 2000.0”. Some of the latter ones incorporate the epoch in their titles, such as “Sky Atlas 2000.0” and “Norton’s 2000.0”.
For this reason, modern star atlases and catalogues always state the epoch for which they were produced, i.e. the particular point in time for which the coordinates given for objects were, or will be, absolutely correct. Most of them use “standard epochs”, which are usually multiples of 50 years; the positions of objects are plotted for the standard epoch closest to the date of publication. So atlases produced between 1925 and 1975 are plotted for “Epoch 1950.0”, i.e. they plot star positions as they were at the start of 1950. Those produced since 1975 are plotted for “Epoch 2000.0”. Some of the latter ones incorporate the epoch in their titles, such as “Sky Atlas 2000.0” and “Norton’s 2000.0”.
 If you need to be really precise, it is of course possible to calculate an object’s true right ascension and declination on a given date, by starting from the values given in a catalogue for a standard epoch, and considering the rates of change of the coordinates. The maths involved in doing this is horribly complicated ( it involves spherical trigonometry ), and probably of no interest except to those studying astrophysics to degree level.
If you need to be really precise, it is of course possible to calculate an object’s true right ascension and declination on a given date, by starting from the values given in a catalogue for a standard epoch, and considering the rates of change of the coordinates. The maths involved in doing this is horribly complicated ( it involves spherical trigonometry ), and probably of no interest except to those studying astrophysics to degree level.
 Of course, no-one actually needs to do those calculations any more; much of today’s astronomical software is capable of taking account of precession, and displaying the sky as it appeared or will appear at any time in the past or future. Those rates of change are very small; for most practical purposes, an Epoch 2000.0 star atlas will be quite close enough, for any time up to 2025.
Of course, no-one actually needs to do those calculations any more; much of today’s astronomical software is capable of taking account of precession, and displaying the sky as it appeared or will appear at any time in the past or future. Those rates of change are very small; for most practical purposes, an Epoch 2000.0 star atlas will be quite close enough, for any time up to 2025.
 This appendix is adapted from an article which I wrote for Transit, the magazine of Cleveland and Darlington Astronomical Society, in 2003. My thanks to my good friend Dr. John McCue, for his invaluable assistance in writing the original.
This appendix is adapted from an article which I wrote for Transit, the magazine of Cleveland and Darlington Astronomical Society, in 2003. My thanks to my good friend Dr. John McCue, for his invaluable assistance in writing the original.
Previous page






 Next page
Next page
Return to Contents
 In Section 5.4, I briefly described the phenomenon of precession, which explains why the astrological “signs” of the Zodiac are now “out of step” with the corresponding constellations, and why the First Point of Aries, also known as the Vernal Equinox, is now in the constellation of Pisces. Here, for the benefit of those readers who might be interested, I’ll attempt to explain the physics of why precession happens.
In Section 5.4, I briefly described the phenomenon of precession, which explains why the astrological “signs” of the Zodiac are now “out of step” with the corresponding constellations, and why the First Point of Aries, also known as the Vernal Equinox, is now in the constellation of Pisces. Here, for the benefit of those readers who might be interested, I’ll attempt to explain the physics of why precession happens.
 As I said in Section 5.4, the Vernal Equinox moves steadily westwards along the Ecliptic at a rate of 50.27 arc seconds per year, completing a full circle every 25800 years. Since the astrologers’ “signs” – which are equal 30° sectors of the Ecliptic - are defined with respect to the Vernal Equinox, this means that they move with respect to the stars at the same rate; hence they move out of step with the constellations, at the rate of one “sign” every ( 25800 / 12 ) years.
As I said in Section 5.4, the Vernal Equinox moves steadily westwards along the Ecliptic at a rate of 50.27 arc seconds per year, completing a full circle every 25800 years. Since the astrologers’ “signs” – which are equal 30° sectors of the Ecliptic - are defined with respect to the Vernal Equinox, this means that they move with respect to the stars at the same rate; hence they move out of step with the constellations, at the rate of one “sign” every ( 25800 / 12 ) years.
 This phenomenon is called the Precession of the Equinoxes, usually just referred to as precession. It was discovered as long ago as 125 BC, by the Greek astronomer Hipparchus. While compiling his famous star catalogue, he found that the star positions recorded in a catalogue from a couple of centuries earlier were consistently in error. He correctly deduced that the relative positions of the Ecliptic and the Celestial Equator are constantly changing, with the Vernal Equinox moving westwards along the Ecliptic at the aforementioned rate. ( The Vernal Equinox, remember, is one of the two points at which the Ecliptic and Celestial Equator intersect. ) The Ecliptic, which is a great circle in the plane of the Earth’s orbit, is fixed with respect to the stars, and the Celestial Equator moves with respect to it.
This phenomenon is called the Precession of the Equinoxes, usually just referred to as precession. It was discovered as long ago as 125 BC, by the Greek astronomer Hipparchus. While compiling his famous star catalogue, he found that the star positions recorded in a catalogue from a couple of centuries earlier were consistently in error. He correctly deduced that the relative positions of the Ecliptic and the Celestial Equator are constantly changing, with the Vernal Equinox moving westwards along the Ecliptic at the aforementioned rate. ( The Vernal Equinox, remember, is one of the two points at which the Ecliptic and Celestial Equator intersect. ) The Ecliptic, which is a great circle in the plane of the Earth’s orbit, is fixed with respect to the stars, and the Celestial Equator moves with respect to it.
 Explaining why this happens had to wait another 1800 years, until Sir Isaac Newton came along! Precession, in general, is a phenomenon which can be easily demonstrated using a simple gyroscope, such as a child’s spinning top. Set the top spinning, then give it a slight nudge so that its axis of rotation tilts away from the vertical – but not far enough to make it topple over! The axis of rotation will then change direction periodically; its direction rotates around the vertical at a constant rate, so that the axis traces out a cone.
Explaining why this happens had to wait another 1800 years, until Sir Isaac Newton came along! Precession, in general, is a phenomenon which can be easily demonstrated using a simple gyroscope, such as a child’s spinning top. Set the top spinning, then give it a slight nudge so that its axis of rotation tilts away from the vertical – but not far enough to make it topple over! The axis of rotation will then change direction periodically; its direction rotates around the vertical at a constant rate, so that the axis traces out a cone.
 This is the reaction of any rotating object when an external torque ( turning effect of two forces ) is applied. In this case, the external torque is provided by gravity, and by the upward reaction of the floor on the base of the top. When the top is tilted, its weight, acting through its centre of mass, exerts a force vertically, at an angle to its axis of rotation ( Fig. 3 ). This force is now displaced horizontally from the upward reaction, and so these two forces – parallel and in opposite directions - create the torque.
This is the reaction of any rotating object when an external torque ( turning effect of two forces ) is applied. In this case, the external torque is provided by gravity, and by the upward reaction of the floor on the base of the top. When the top is tilted, its weight, acting through its centre of mass, exerts a force vertically, at an angle to its axis of rotation ( Fig. 3 ). This force is now displaced horizontally from the upward reaction, and so these two forces – parallel and in opposite directions - create the torque.
 This torque can’t speed up or slow down the top, but can change its direction of spin – just as the tension in the string of a whirling conker doesn’t change its speed, but does continually change its direction of motion, thus making it follow a circle. The directional effect of the torque is at right angles to itself, which means it’s perpendicular to the plane formed by the spin axis and the vertical. This causes the axis to precess, or rotate around the vertical.
This torque can’t speed up or slow down the top, but can change its direction of spin – just as the tension in the string of a whirling conker doesn’t change its speed, but does continually change its direction of motion, thus making it follow a circle. The directional effect of the torque is at right angles to itself, which means it’s perpendicular to the plane formed by the spin axis and the vertical. This causes the axis to precess, or rotate around the vertical.


